Câu I: (2 điểm)

Một công ty có 3 ca làm việc, trong đó có 1000 công nhân làm việc ca sáng, 700 công nhân làm việc ca chiều, 300 công nhân làm việc ca tối, xác suất một công nhân vắng mặt trong các ca làm việc sáng, chiều, tối tương ứng 0,02; 0,05; 0,07

1)    Tính tỉ lệ công nhân làm việc trong toàn bộ công ty

2)    Có một công nhân đã không làm việc, xác suất người này thuộc nhóm làm việc ca chiều là bao nhiêu

Đáp Án

1.    Tính tỉ lệ công nhân làm việc trong toàn bộ công ty

Tổng số công nhân trong công ty là:

     1000 + 700 + 300 = 2000

Do đó, tỉ lệ công nhân làm việc trong từng ca là:

Ca sáng: 1000/2000 = 0.5

Ca chiều: 700/2000 = 0.35

Ca tối: 300/2000 = 0.15

2.    Xác suất công nhân không làm việc thuộc ca chiều

Cho biết xác suất một công nhân vắng mặt trong các ca làm việc sáng, chiều, tối tương ứng là 0.02; 0.05; 0.07. Chúng ta sẽ sử dụng định lý Bayes để tính xác suất một công nhân vắng mặt thuộc ca chiều.

Trước hết, tính xác suất tổng hợp để một công nhân bất kỳ không làm việc:

P(V) = P(V∣S)P(S)+P(V∣C)P(C)+P(V∣T)P(T)

Trong đó:

-       P(V∣S) là xác suất vắng mặt nếu công nhân thuộc ca sáng = 0.02

-       P(V∣C) là xác suất vắng mặt nếu công nhân thuộc ca chiều = 0.05

-       P(V∣T) là xác suất vắng mặt nếu công nhân thuộc ca tối = 0.07

-       P(S) là xác suất công nhân thuộc ca sáng = 0.5

-       P(C) là xác suất công nhân thuộc ca chiều = 0.35

-       P(T) là xác suất công nhân thuộc ca tối = 0.15

Vì vậy:

P(V)=0.02×0.5+0.05×0.35+0.07×0.15

P(V)=0.01+0.0175+0.0105

P(V)=0.038

Tiếp theo, tính xác suất một công nhân vắng mặt thuộc ca chiều:

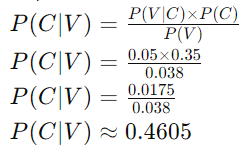
Vậy xác suất một công nhân đã không làm việc thuộc nhóm làm việc ca chiều là khoảng 0.4605 (hay 46.05%).

Câu II: (1,5 điểm)

Chi phí cho quảng cáo và doanh thu của công ty lần lượt là các biến ngẫu nhiên X và Y( đơn vị: triệu đồng ) . Giả sử (X;Y) có bảng phân phối xác suất như sau:

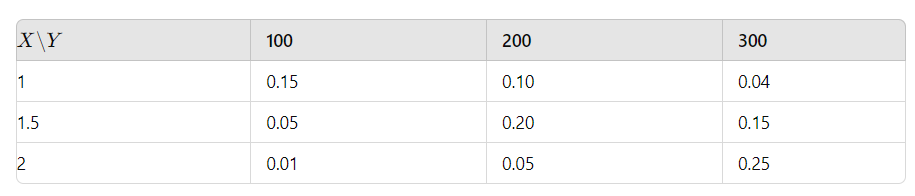
1. Tính P( Y= 200)
2. Nếu chi phí cho quảng cáo là 1,5 triệu đồng thì trung bình của doanh thu là bao nhiêu?
3. Tính E(X)

Đáp Án

1)   Tính P( Y= 200)