Câu I ( 2 điểm)

   Một người đi mua hàng tại một trong ba nơi với tỉ lệ chọn một trong ba nơi trên là như nhau, Nếu người đó đến nơi thứ nhất, xác suất mua được hàng là 0,7 , nếu người đó đến nơi thứ hai xác suất mua được hàng là 0,5 nếu người đó đến nơi thứ ba xác suất mua được hàng là 0,25

a)    Tính xác suất người đó mua được hàng

b)    Biết người đó mua được hàng tính xác suất người đó đến nơi thứ ba

Đáp án

a) Tính xác suất người đó mua được hàng

Giả sử:

-       A1 là sự kiện người đó đến nơi thứ nhất, P(A1) = ⅓

-       A2 là sự kiện người đó đến nơi thứ hai, P(A2) = ⅓

-       A3 là sự kiện người đó đến nơi thứ ba, P(A3) = ⅓

-       B là sự kiện người đó mua được hàng

Theo định lý xác suất toàn phần, xác suất người đó mua được hàng là:

          P(B)=P(B∣A1​)P(A1​)+P(B∣A2​)P(A2​)+P(B∣A3​)P(A3​)

Với các xác suất có điều kiện đã cho:

-       P(B∣A1​)=0.7

-       P(B∣A2​)=0.5

-       P(B∣A3​)=0.25

Vậy ta có:

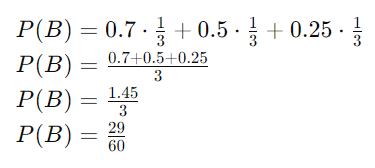
b) Biết người đó mua được hàng, tính xác suất người đó đi đến nơi thứ ba

 Sử dụng định lý Bayes, ta có:

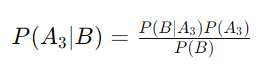
Thay các giá trị vào:

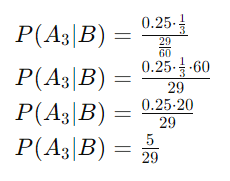
Vậy xác suất người đó đi đến nơi thứ ba biết rằng họ đã mua được hàng là:

Câu II ( 1,5 điểm )

 Nhu cầu về một loại hàng hóa là biến X có bảng phân phối xác suất như sau :

cửa hàng nhập về 340 sản phẩm để bán. Tính kỳ vọng của số sản phẩm bán được

Đáp Án

 Kỳ vọng của số sản phẩm bán được E(X) được tính bằng công thức:

              E(X)=∑i​Xi​⋅P(Xi​)

Với các giá trị cụ thể:

             E(X)=300⋅0.1+320⋅0.15+340⋅0.25+360⋅0.5

Ta tính từng phần:

       300*0,1=30

       320*0,15=48

       340*0,25=85

       360*0,5= 180

Sau đó, tổng hợp lại:

                  E(X)=30+48+85+180=343

Vậy kỳ vọng của số sản phẩm bán được là 343.

Câu III (1,5 điểm)