PHẦN 1: XÁC SUẤT

Chương 1: Biến cố và phép tính xác suất

       I.          Giải tích tổ hợp

1.     Quy tắc cộng và quy tắc nhân

*         Quy tắc cộng: Một hành động H xảy ra khi và chỉ khi có một trong k hành động Hi xảy ra ( i =  ) (Hi và Hj không đồng thời xảy ra). Hành động H được gọi là tuân theo quy tắc cộng. Nếu hành động Hi có mi cách chọn thì H có m1 + m2 + …+mk cách chọn H.

*         Quy tắc nhân: Một hành động H xảy ra khi và chỉ khi đồng thời k hành động Hi xảy ra ( i =  ). Hành động H được gọi là tuân theo quy tắc nhân. Nếu hành động Hi có mi cách chọn thì H có m1. m2 …mk cách chọn H.

 

2.     Hoán vị

Mỗi cách sắp xếp n phần tử khác nhau theo một thứ tự nhất định được gọi là một hoán vị của n phần tử đó. Số hoán vị: P_n = 1.2.3…n = n!. Quy ước: 0! =1

 

3.     Chỉnh hợp

Cho tập X = {x₁, x₂ , ..., x_n};1≤ k ≤  n . Sắp xếp k phần tử của tập X theo một thứ tự nhất định được một chỉnh hợp chập k của X. Số chỉnh hợp: A^k =n!/(n - k)!

 

4.     Tổ hợp

Cho tập X = {x1, x2 , ..., xn};1≤ k ≤  n. Mỗi tập con có k phần tử của tập X được gọi là một tổ hợp chập k của n của X. Số tổ hợp  C_n^k =n!/k!(n - k)! = A_n^k /k!

 

5.     Chỉnh hợp lặp

Chỉnh hợp lặp chập k của n phần tử là một bộ có thứ tự k phần tử chọn từ tập hợp X có n phần tử. Lưu ý rằng mỗi phần tử có thể xuất hiện nhiều lần.

Số chỉnh lặp:  A_n^k  = n^k

 

6.     Nhị thức Newton

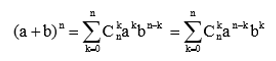
     II.          Biến cố ngẫu nhiên và quan hệ giữa các biến cố ngẫu nhiên

1.     Phép thử và biến cố

Việc thực hiện một nhóm các điều kiện cơ bản để quan sát một hiện tượng nào đó xảy ra hay không được gọi là thực hiện một phép thử, còn hiện tượng có thể xảy ra trong kết quả của phép thử được gọi là biến cố.

Phép thử, ký hiệu: T

Biến cố, ký hiệu: A, B, C, …

 

2.     Các loại biến cố

Giả sử thực hiện một phép thử nào đó, ta có các loại biến cố sau:

*  Biến cố chắc chắn: Biến cố chắc chắn là biến cố nhất định xảy ra trong phép thử, ký hiệu là U.

*  Biến cố không: Biến cố không là biến cố không thể xảy ra trong phép thử, ký hiệu là V.

Ví dụ 4. Trong phép thử ở ví dụ 3. Biến cố “mặt xuất hiện có số chấm nhỏ hơn 7” là biến cố U, biến cố “mặt xuất hiện có số chấm bằng 7” là biến cố V.

*  Biến cố ngẫu nhiên: Các biến cố có thể xảy ra hoặc không thể xảy ra khi thực hiện phép thử được gọi là biến cố ngẫu nhiên.

Ví dụ 5. Các biến cố ở ví dụ 1, ví dụ 2, ví dụ 3 là các biến cố ngẫu nhiên.

*  Biến cố sơ cấp: Một phép thử được xác định bằng một tập hợp các kết quả cụ thể của nó, các kết quả này là các kết quả nhỏ nhất của phép thử mà không thể chia nhỏ được hơn nữa. Các kết quả này được gọi là các biến cố sơ cấp. Tập hợp các biến cố sơ cấp được gọi là không gian xác suất Ω = {ωi; i =1,...,n}

*  Biến cố đồng khả năng: Biến cố đồng khả năng là các biến cố có cùng khả năng xuất hiện như nhau trong một phép thử.

 

 

3.     Phép toán và quan hệ giữa các biến cố

a.  Tổng của các biến cố

Tổng của hai biến cố A và B là biến cố xuất hiện khi ít nhất A hoặc B xuất hiện, ký hiệu A + B.

Tổng của n biến cố A₁, A₂, …, A_n là biến cố xuất hiện khi ít nhất một biến cố A_i ( i = 1, 2,..., n ) xuất hiện, ký hiệu A₁ + A₂ + … + A_n.

b.  Tích của các biến cố

Tích của hai biến cố A và B là biến cố xuất hiện khi đồng thời A và B xuất hiện, ký hiệu AB.

Tích của n biến cố A₁, A₂, …, A_n là biến cố xuất hiện khi đồng thời n biến cố A_i ( i = 1, 2,..., n ) xuất hiện, ký hiệu A₁A₂ …A_n.

c.  Hiệu hai biến cố

Hiệu của hai biến cố A và B là biến cố xuất hiện khi đồng thời A xuất hiện và B không xuất hiện, ký hiệu A\B.

d.  Biến cố đối lập

Biến cố đối lập của A là biến cố không xuất hiện A, ký hiệu  .

Hiển nhiên ta có: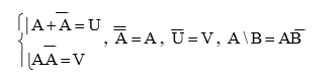

e.  Phép kéo theo, phép tương đương

Biến cố A kéo theo B nếu A xuất hiện thì B xuất hiện, ký hiệu A | B

Nếu A kéo theo B và B kéo theo A thì A tương đương với B, ký hiệu A = B. Hay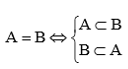 

f.  Biến cố xung khắc

Hai biến cố A và B được gọi là xung khắc nếu chúng không đồng thời xuất hiện, ký hiệu AB = V.

g.  Các tính chất

Giống như các tính chất trên tập hợp, các phép toán trên các biến cố có tác tính chất sau:

*  Giao hoán:

A + B = B +A              AB = BA

*  Kết hợp:

(A + B) + C = A + (B + C)                 (AB)C = A(BC)

*  Phân phối:

A(B + C) = AB + AC               (A+ B)C = AC + BC

*  Một số tính chất khác

 

                   

 

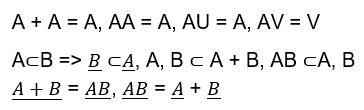
4.     Hệ đầy đủ của các biến cố

Dãy n biến cố {B₁, B₂, …, B_n} được gọi là hệ đầy đủ n biến cố nếu thỏa mãn:

i)  Các biến cố của hệ xung xung từng đôi một: B_iB_j = V (i ≠ j)

ii)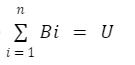

 

   III.          Định nghĩa xác suất của biến cố

1.     Định nghĩa cổ điển về xác suất

Trong phép thử T có xuất hiện biến cố A. Trong đó, có n kết cục duy nhất đồng khả năng và có m kết cục thuận lợi cho biến cố A. Khi đó, xác suất của biến cố A, ký hiệu

P(A) được xác định như sau: P(A) = m/n

Tính chất:

i)  

ii)  P(U) = 1

iii)  P(V) = 0

iv)   A ⊂ B =>  P(A)⊂ P(B)

 

2.     Định nghĩa thống kê của xác suất

Giả sử tiến hành n phép thử cùng loại, trong mỗi phép thử có thể xuất hiện hoặc không xuất hiện biến cố A, gọi k là số phép thử xuất hiện biến cố A trong n phép thử.

Khi đó, tần suất xuất hiện biến cố A trong n phép thử đã cho là f_n(A) = k/n

Xác suất của biến cố A là giới hạn của tần suất khi số phép thử tăng lên vô hạn:

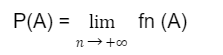
Khi n khá lớn, với sai số cho phép có thể lấy f_n(A) thay thế cho P(A).

3.     Định nghĩa hình học của xác suất

Để mở rộng định nghĩa xác suất cho phép thử có vô hạn kết cục đồng khả năng. Người ta đưa vào định nghĩa hình học của xác suất.

Cho miền G trong mặt phẳng (đường thẳng, không gian 3 chiều, …) và một miền con

đo được g của G. Gọi A là biến cố lấy ngẫu nhiên một điểm thì điểm đó thuộc g. Khi

đó, xác suất của A xác định bởi: P(A) = S(g)/S(G)

S(g) là độ đo của g, S(G) là độ đo của G.

Chú ý 1. Khái niệm độ đo được hiểu như sau:

-       Nếu G nằm trong đường thẳng thực R thì độ đo chính là độ dài.

-       Nếu G nằm trong mặt phẳng R² thì độ đo chính là diện tích.

-       Nếu G nằm trong không gian R³ thì độ đo chính là thể tích.

Chú ý 2. Các bài toán tính xác suất muốn áp dụng định nghĩa hình học đều phải chuyển về hoặc độ dài, hoặc diện tích, thể tích của g, G.

 

4.     Nguyên lí xác suất nhỏ, xác suất lớn

*         Nguyên lý xác suất nhỏ: Một biến cố có xác suất rất nhỏ bằng ∝ (gần bằng 0) có thể cho rằng trong thực tế nó không xảy ra trong phép thử.  ∝ thường gọi là mức ý nghĩa:  ∝= 0,1;   0, 05;   0, 01;...

*         Nguyên lý xác suất lớn: Một biến cố có xác suất lớn bằng β  (gần bằng 1) có thể cho rằng trong thực tế nó nhất định xảy ra trong phép thử. β  thường gọi là độ tin cậy:

β =  0, 99;  0, 95;  0, 90;...

 

 

  IV.          Công thức tính xác suất

1.     Xác suất có điều kiện

Định nghĩa 1: Xác suất của biến cố A được tính với giả thiết biến cố B đã xảy ra gọi là xác suất của A với điều kiện B, ký hiệu: P(A/B) hoặc P(A/B)
 Định nghĩa 2. Hai biến cố A và B được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng gì đến việc xảy ra hay không xảy ra của biến cố kia và ngược lại.

    Nói cách khác, A và B độc lập nếu P(A/B) = P(A) = P(A / B) và  P(B/A) = P(B) = P(B / A) . Hai biến cố A và B không độc lập được gọi là phụ thuộc nhau.

Định nghĩa 3.

+) Các biến cố A₁, A₂, …, A_n được gọi là độc lập từng đôi nếu mỗi cặp biến cố bất kỳ trong chúng độc lập với nhau.

+) Các biến cố A₁, A₂, …, A_n được gọi là độc lập toàn phần (độc lập trên toàn thể) nếu mỗi biến cố trong chúng độc lập với tổ hợp của một số bất kỳ các biến cố còn lại.

 

2.     Công thức nhân xác suất

Cho A và B là hai biến cố trong một phép thử. Từ định nghĩa xác suất, ta chứng minh được định lý sau:

Định lý 1. P(AB) = P(A).P(A/B) = P(B). P(B/A)

Hệ quả 1. i) Nếu P(B) > 0 thì P(A / B) = P(AB)

ii) Nếu P(A) > 0 thì P(B / A) = P(AB)/P(A)

Hệ quả 2. A và B độc lập =>  P(AB) = P(A).P(B)

Bằng quy nạp có thể tổng quát định lý nhân xác suất với n biến cố như sau:

Định lý 2. Nếu P(A₁A₂ … A_n-1) > 0 thì

P(A₁A₂ … A_n) = P(A₁). P(A₂/A₁) … P(A_n/A₁A₂ … A_n-1)

Hệ quả 3. Nếu các biến cố A₁, A₂, …, A_n độc lập toàn phần thì ta có P(A₁A₂ … A_n) = P(A₁). P(A₂) … P(A_n)

 

3.     Công thức cộng xác suất

Định lý 3. P(A + B) = P(A) + P(B) – P(AB)

Hệ quả 1. Nếu A và B là hai biến cố xung khắc thì P(A + B) = P(A) + P(B) Tổng quát, nếu n biến cố A₁, A₂, …, A_n xung khắc từng đôi một thì ta có:

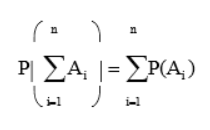
Nếu A₁, A₂, …, A_n là hệ đầy đủ n biến cố thì 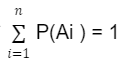 P(Ai ) = 1

Hệ quả 2. P() = 1- P(A)