Chương 1: Mô hình định tuyến và đại số ma trận

I.         Ma trận

1.    Khái niệm

a.    Ma trận cấp m x n : là một bảng gồm mn số aij được sắp xếp thành m dòng và n cột dưới dạng

 

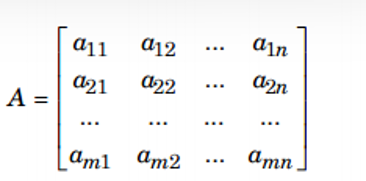
b.    Ma trận vuông: là ma trận có số dòng m bằng số cột n, khi đó thay vì nói ma trận cấp n x n ta chỉ nói đó là ma trận vuông cấp n.

 

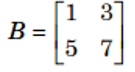
c.     Ma trận đơn vị: là ma trận vuông có tất cả các phần tử thuộc đường chéo chính đều bằng 1, các phần tử còn lại đều bằng 0, kí hiệu là In

 

 

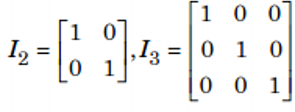
d.    Ma trận tam giác: là ma trận vuông có tất cả các phần tử nằm phía dưới, hoặc phía trên đường chéo chính đều bằng 0

 

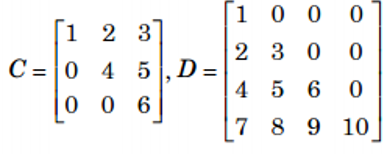
e.    Ma trận chéo: là ma trận vuông có tất cả các phần tử nằm ngoài đường chéo chính đều bằng 0.

 

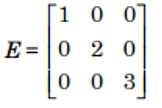
f.      Ma trận cột: là ma trận chỉ có một cột

Ma trận dòng: là ma trận chỉ có một dòng.

 

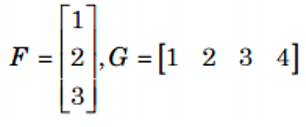
g.    Ma trận không: là ma trận có tất cả các phần tử đều bằng 0, kí hiệu là Omxn

 

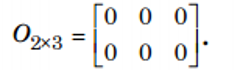
h.    Ma trận bậc thang: là ma trận thoả mãn hai điều kiện sau đây

- dòng có tất cả các phần tử bằng 0 (nếu có) nằm phía dưới dòng có phần tử khác 0;

- phần tử khác 0 đầu tiên (tính từ trái sang phải) của mỗi dòng dưới nằm bên phải so với phần tử khác 0 đầu tiên của dòng trên

                             

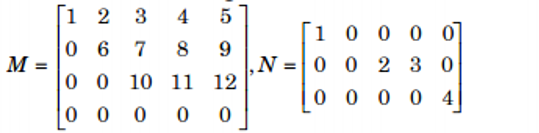
2.    Các phép toán trên ma trận

a.    Tổng hai ma trận cùng cấp

 

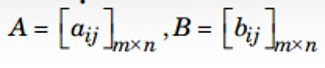
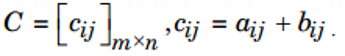
b.    Tích của một số với một ma trận bất kì

 

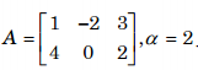
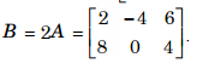
c.     Tích của hai ma trận

 

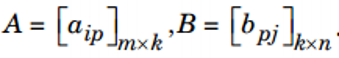
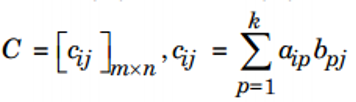
d.    Phép chuyển vị

 

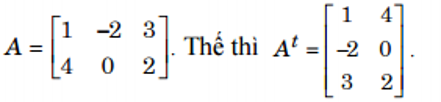
e.    Luỹ thừa một ma trận vuông

Luỹ thừa bậc n của ma trận A là tích của n ma trận A , nghĩa là ... Aⁿ =  AA… A (n lần).

 

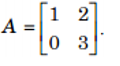
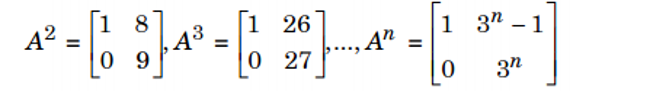
3.    Các tính chất

A + B = B + A ,A + O = A, A + (– A ) = O ,

A + (B + C ) = (A + B ) + C, A(BC ) = ( AB)C, 1A = A, AI = IA = A,(αβ ) A = α( β A),

(α + β ) A = α A + β A,α( A + B) = α A + α B.

 

II.         Định thức

1.    Khái niệm

a.     Định thức cấp một: là định thức của ma trận vuông cấp một A = [a11] .

Khi đó ta có det A = a11 = a11 .

Ví dụ 1. A = [4], detA = 4; B = [ –3],det B = –3 .

b.    Định thức cấp hai: là định thức của ma trận vuông cấp hai

 

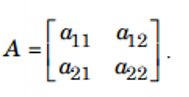
Khi đó detA:

 

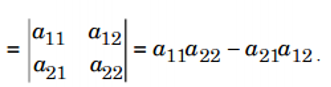
c.     Định thức cấp ba: là định thức của ma trận vuông cấp ba

 

 

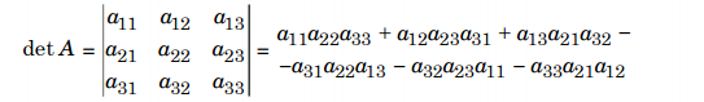
d.    Định thức con bù - phần bù đại số

=> Phần bù đại số của phần tử aij:

 

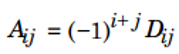
e.    Định thức cấp n

 

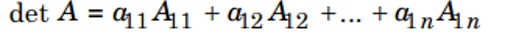
2.    Các tính chất

Định thức cấp bất kì có các tính chất sau đây.

-       det A = det At (Hai ma trận chuyển vị có định thức bằng nhau).

-       Định thức có một dòng bằng 0 thì bằng 0.

-       Định thức có hai dòng giống nhau hoặc tỉ lệ với nhau thì bằng 0.

-       Nhân tử chung của một dòng có thể đem ra ngoài định thức.

-       Định thức của ma trận tam giác bằng tích các phần tử thuộc đường chéo chính.

-       Nếu đổi chỗ hai dòng bất kì thì định thức đổi dấu.

-       Định thức không hay đổi, nếu cộng vào một dòng các phần tử tương ứng của dòng khác đã được nhân với cùng một số.

-       Các tính chất trên vẫn đúng khi thay chữ “dòng” bởi chữ “cột”.

-        Công thức định nghĩa định thức cấp n vẫn đúng khi thay dòng 1 bởi dòng bất kì khác, nghĩa là: det A = ai1Ai1 + ai2 Ai2 + ... + ain Ain , i = 1,2,..., n.

-       Tương tự ta có công thức khai triển định thức theo cột bất kì: det A = a1 j A1 j + a2 j A2 j + ... + anj Anj, j = 1,2,..., n.

 

III.         Ma trận nghịc đảo

1.    Khái niệm

Định nghĩa: Cho

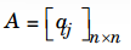
là ma trận vuông cấp n. Ma trận B thỏa mãn điều kiện AB = BA = In được gọi là ma trận nghịch đảo của A và kí hiệu là B = A^–1 .

Ví dụ 1.

 

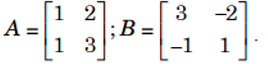
Khi đó ta có AB = BA = I2 nên B = A–1 .

Chú ý: Nếu B = A– 1 thì A = B–1 . Do đó ta còn nói A và B là các ma trận nghịch đảo của nhau.

Định nghĩa: Nếu ma trận A có ma trận nghịch đảo A–1 thì ta nói A là ma trận khả nghịch, hay khả đảo.

 

2.    Điều kiện khả nghịch

Định lý: Để ma trận vuông A khả nghịch, cần và đủ là det A ≠ 0.

 

3.    Phương pháp tìm ma trận nghịch đảo

-       Định thức

●      Tính detA

●      Tính phần bù đại số

●      Lập ma trận từ phần bù đại số

●      Tính ma trận nghịch đảo

 Ví dụ

 

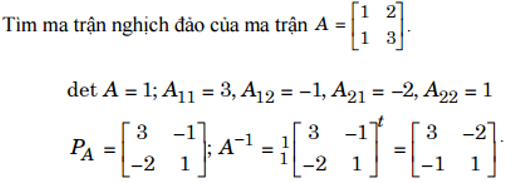
-       Các phép biến đổi sơ cấp đối với ma trận bất kì:

●      Đổi chỗ hai dòng tuỳ ý của ma trận.

●      Nhân tất cả các phần tử của một dòng với một số khác 0.

●      Cộng vào một dòng các phần tử tương ứng của dòng khác đã được nhân với cùng một số.

-       Tìm ma trận nghịch đảo bằng phương pháp biến đổi sơ cấp

 

  IV.         Hạng của ma trận

1.    Khái niệm

-       Định thức gồm các phần tử thuộc giao của k dòng và k cột tuỳ ý của A được gọi là định thức con cấp k của A

Ví dụ:

                       

 

Ngoài ra ma trận A còn có 3 định thức con cấp ba khác, tất cả các định thức con cấp ba của A đều bằng 0. Các định thức con cấp cao hơn không tồn tại.

-       Hạng của ma trận: Ta nói hạng của ma trận Alà p nếu trong Acó ít nhất một định thức con cấp p khác 0, các định thức con cấp cao hơn đều bằng 0 hoặc không tồn tại.

Khi đó ta viết rank( A)  p hoặc r( A)  p.