1.  Các công thức tính xác suất

1.1 Công thức cộng xác suất tổng quát:

Nếu các biến cố A1,A2…An ( (n ≥ 2)) liên quan đến cùng một phép thử thì

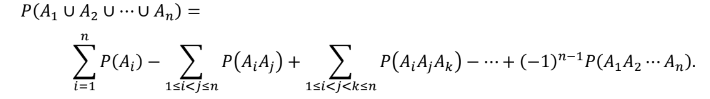
Nếu thêm giả thiết A1,A2,...An đôi một xung khắc thì

1.2 Xác suất có điều kiện:

  Giả sử P(A) > 0. Xác suất có điều kiện của biến cố B với điều kiện biến cố A đã xảy ra là P(B| A):

ta có : P(B|A) +P(B̅|A) =1

1.3 Công thức Nhân xác suất tổng quát:

Nếu các biến cố A1, A2, ... , An (n ≥ 2) liên quan đến cùng một

phép thử và P(A1A2 ⋯ An−1) > 0 (n ≥ 2), thì

P(A1A2 ⋯ An) = P(A1)P(A2|A1)P(A3|A1A2) ⋯ P(An|A1A2 ⋯ An−1)

 +Nếu hai biến cố A1, A2 liên quan đến cùng một phép thử và độc lập thì P(A1A2) = P(A1)P(A2).

 +Nếu các biến cố A1, A2, ... , An (n ≥ 3) liên quan đến cùng một phép thử và độc lập toàn phần thì P(A1A2 ⋯ An) = P(A1)P(A2)P(A3) ⋯ P(An).

1.4 Công thức Xác suất đầy đủ, công thức Bayes:

Nếu H1, H2, ... , Hn là một nhóm đầy đủ các biến cố và A

là một biến cố trong cùng một phép thử với P(A) > 0, P(Hi) > 0, ∀i ∈ {1; ... ; n}, thì:

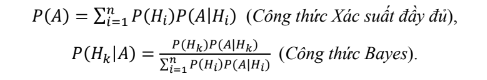
2. Một số đặc trưng của biến ngẫu nhiên:

 • Mode của biến ngẫu nhiên X, kí hiệu bởi mod(X), là số thực x∗ được xác định như

sau:

- Nếu X là biến ngẫu nhiên rời rạc với luật phân phối xác suất cho bởi P{X = xj} = pj, thì P{X = x∗} là số lớn nhất trong tất cả các số pj

- Nếu X là biến ngẫu nhiên liên tục thì x∗là điểm tại đó hàm mật độ đạt cực đại.

• Kỳ vọng của biến ngẫu nhiên X, kí hiệu bởi E(X), là một số được xác định như sau:

- Nếu X là biến ngẫu nhiên rời rạc thì E(X) =  

- Nếu X là biến ngẫu nhiên liên tục với hàm mật độ f(x) thì E(X) =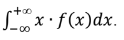

• Phương sai của biến ngẫu nhiên X